Advent of Code 2025 Day 9 Part 2 Explained - Movie Theater
You can find my Rust implementation on Github.
The first tricky one of this year, but actually not that tricky!
Part 1
Nothing difficult here. Since there are no constraints on the rectangles you can build, you just check every pair of coordinates and compute the rectangle areas to find the largest one.
Part 2
This is where things get tricky.
..............
.......#...#..
..............
..#....#......
..............
..#......#....
..............
.........#.#..
..............
..............
.......#XXX#..
.......X...X..
..#XXXX#...X..
..X........X..
..#XXXXXX#.X..
.........X.X..
.........#X#..
..............
..............
.......#XXX#..
.......XXXXX..
..#XXXX#XXXX..
..XXXXXXXXXX..
..#XXXXXX#XX..
.........XXX..
.........#X#..
..............
In Part 1 we only had the red tiles #, and no constraints.
Now we also have the green tiles X, which:
- connect the red tiles together, forming a border and closing the shape
- fill the entire inside of that shape
The rectangle that we are looking for must be made only of red and green tiles. It essentially means it has to lie completely inside the closed shape.
At first it looks complicated, especially given the size of the grid and the number of coordinates.
But remember this: you don’t need a generic solution. You just need a solution that works for your input.
I didn’t know where to start.
When I don’t know where to start, I like to draw things on paper.
But here my room is too small for these coordinates, so instead I used a tool to plot all the points from my input.
And here’s what I got:
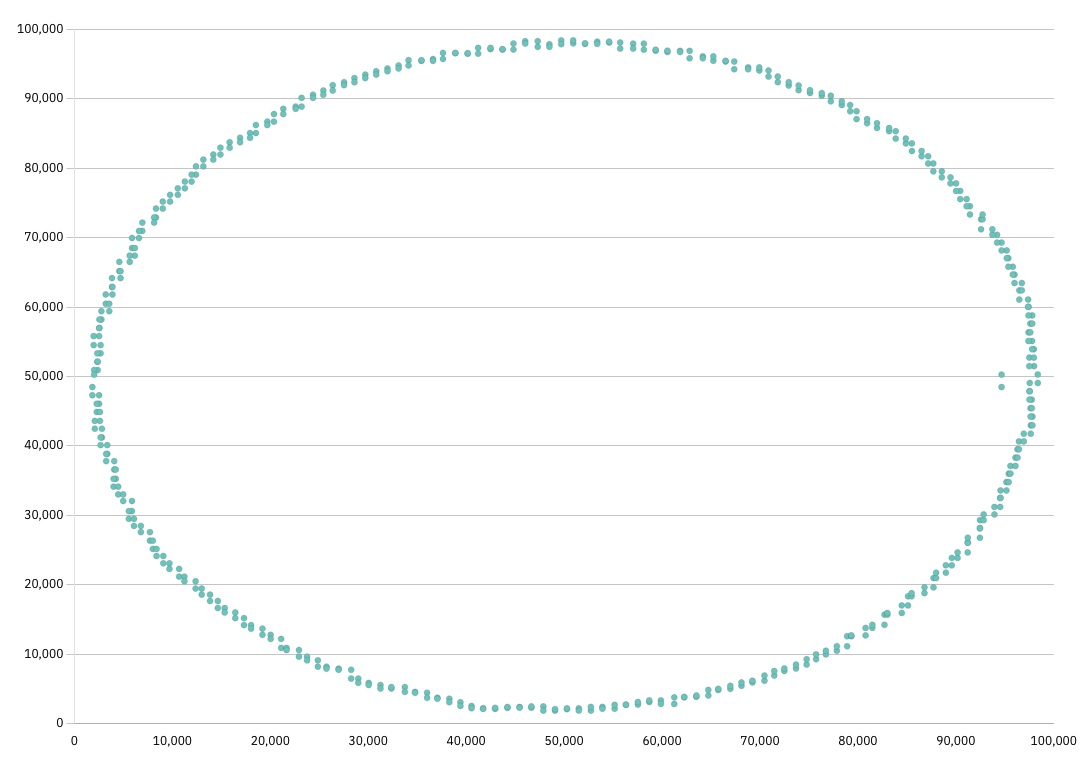
It looks like a very special case.
When you see this kind of input, you know they’re not expecting you to build a generic solution.
We have a big circle-like shape with multiple layers of points, and 2 dots on the same vertical line at the right inside the circle.
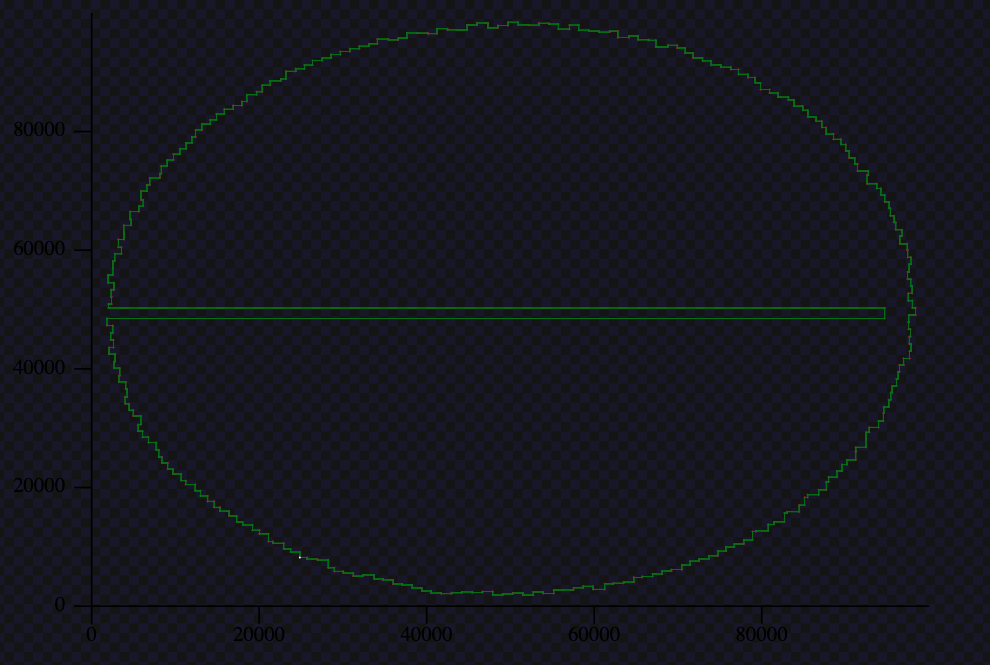
Then, I drew the green tiles making the borders. Something interesting appeared: there’s a big “no man’s land” right in the middle. It’s impossible to form a rectangle that crosses this center area, because it would include cells that are neither green nor red.
This immediately tells us the rectangle has to be in the top half or in the bottom half.
There is a tiny connection between the two halves on the right, but it’s too narrow. No chance the largest rectangle hides there.
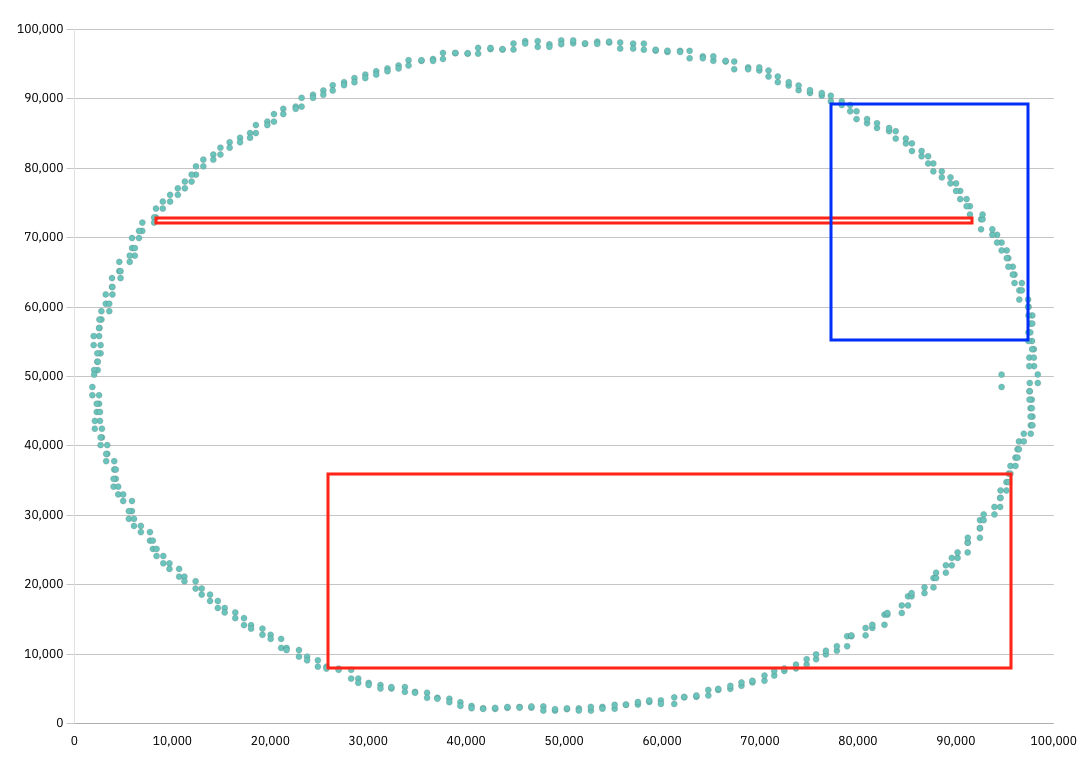
Now let’s do a simple experiment.
Try drawing a big rectangle, either in the top half or the bottom half, using any two coordinates of the circle as opposite corners.
You’ll quickly notice something: one of the corners always ends up outside the circle.
This happens simply because of the geometry of the circle.
There are a few exceptions, like for narrow rectangles. But these will never be the big rectangle we are looking for.
So how do we solve this problem?
- We’re given a circle of dots
- We must use two dots as opposite corners of the rectangle
- The rectangle has to stay inside the circle (because only red/green tiles are allowed)
- And because the shape is a circle, it feels impossible
It’s time to look at these 2 dots.
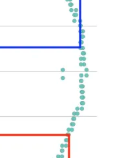
One is part of the top half. The other is part of the bottom half.

And if you try to use these inner dots as the bottom-right corner (for rectangles in the top half) or the top-right corner (for rectangles in the bottom half), you get plenty of big valid rectangles!
So my guess was:
- To find the biggest rectangle in the top half, use the top inner dot as the bottom-right corner
- To find the biggest rectangle in the bottom half, use the bottom inner dot as the top-right corner
Then take the biggest of the two, and that’s the answer.
And it turned out to be a valid guess: I got the correct answer with that solution.
But there’s one thing left to figure out: How do we check that the rectangle contains only red and green tiles?
Using these two inner dots gives you lots of valid rectangles, but also plenty of invalid ones. So we still need to verify each rectangle.
If you look back at the image where I drew the rectangles, you’ll notice that whenever a rectangle goes out of bounds, it’s always a full corner that is out: one vertical side and one horizontal side.
But we don’t actually need to check both sides.
It’s enough to check whether a vertical side crosses a horizontal green border.
By horizontal green border, I mean a horizontal line of green tiles between two red tiles on the border of the shape, like this:
..............
.......#XXX#..
..............
How?
I created a Map where:
- the key is the x-coordinate
- the value is a list of all y-coordinates where a horizontal border of green tiles exists at that x
When I want to verify whether a rectangle is valid, I check each of its vertical sides.
A vertical side has two important points: the top and the bottom (corners of the rectangle).
Since both share the same x-coordinate, I look up the list of green-border y-values for that x in the hashmap.
If there exists a tile tile_y such that side_top_y > tile_y > side_bot_y then the side crosses a horizontal green border — meaning the rectangle goes out of bounds — and therefore the rectangle is invalid.
And that’s it!
Hope it helps.